OTIMIZAÇÃO DOS PARÂMETROS GEOMÉTRICOS DE UM CAMO
L. Germanio (1) e R. L. U. de F. Pinto (1)
(1)Departamento de Engenharia Mecânica, Escola de Engenharia, Universidade Federal de Minas Gerais, Av. Antônio Carlos, 6627, Pampulha, Belo Horizonte MG, CEP: 31270-901
Palavras Chaves: geometria de um camo, modelagem, otimização
RESUMO
O conjunto constituído por um camo e um seguidor do tipo rolete (vide figura 1) tem sido o mecanismo mais utilizado para transformar um movimento giratório em um movimento translacional alternativo. A superfície do camo deve ter uma curva R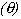 tal que proporcione ao seguidor uma curva de deslocamento h
tal que proporcione ao seguidor uma curva de deslocamento h especificada. Neste trabalho apresenta-se um procedimento para a otimização de um camo utilizando um algoritmo de programação matemática.
especificada. Neste trabalho apresenta-se um procedimento para a otimização de um camo utilizando um algoritmo de programação matemática.
|
Inicialmente, identificou-se quais os requisitos indispensáveis ao funcionamento adequado do mecanismo e quais as características mais desejáveis. Detectou-se que para este mecanismo são desejáveis pequeno perímetro, pequeno momento de inércia e uma geometria que respeitasse um limite preestabelecido para a tensão superficial. Assim, construiu-se uma função objetivo que permitisse a minimização do perímetro do camo ou da sua inércia, ou mesmo de uma combinação de ambos, com um termo de penalidade para forçar que a tensão superficial tenha um valor preestabelecido. |
De acordo com Mabie e Reinholtz (1985), Chen (1982) e Johnson (1985), obteve-se para a modelagem do mecanismo, as seguintes equações:
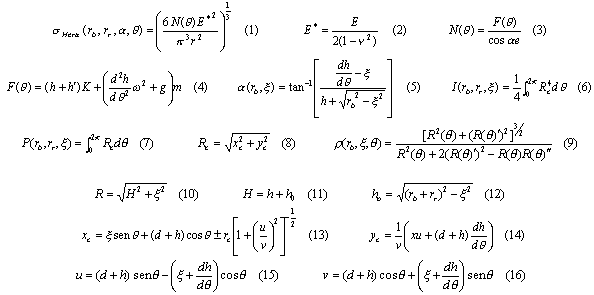
onde h', K, ![]() , g, m E, v,
, g, m E, v, ![]() , ks e
, ks e ![]() são constantes que representam, respectivamente, a pré-deformação da mola, a constante elástica da mola, a velocidade angular, a aceleração da gravidade, a massa acionada, o módulo de elasticidade do material, o coeficiente de Poison, o coeficiente de segurança e a excentricidade. rb e rr denotam o raio da circunferência de base e o raio do rolete, os parâmetros a serem otimizados.
são constantes que representam, respectivamente, a pré-deformação da mola, a constante elástica da mola, a velocidade angular, a aceleração da gravidade, a massa acionada, o módulo de elasticidade do material, o coeficiente de Poison, o coeficiente de segurança e a excentricidade. rb e rr denotam o raio da circunferência de base e o raio do rolete, os parâmetros a serem otimizados.
Dentro da estratégia de penalidade, formulou-se o seguinte problema de otimização:
![]()
onde os valores de I e P são obtidos a partir das equações (6) e (7). Os coeficientes k1 e k2 representam pesos para as respectivas parcelas. Assim, adotando-se k2 = 0 tem-se o problema de minimizar a inércia. Por outro lado, adotando-se k1 = 0 tem-se o problema de minimizar o perímetro. Outras combinações de k1 e k2 representam uma minimização ponderada das duas parcelas. O último termo representa a penalização pela violação da igualdade (1).
Para a solução numérica do problema de otimização, utilizou-se o método de Fletcher-Reeves, conforme Luenberger (1989), implementado através do MATLAB 5.2.0. As restrições de desigualdade foram ignoradas na implementação do algoritmo, sendo verificadas a posteriori.
Adotou-se para a lei de deslocamento da haste:
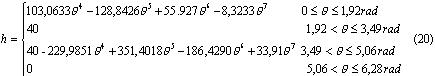
Resultados foram obtidos conforme as Tabelas 1 e 2. Na Figura 2 vê-se o perfil obtido para o ponto inicial (rb = 80,rr = 20) (curva marcada por *) e o valor otimizado (rb = 41,57; rr 10,82) (curva marcada com +), conforme a Figura 2.
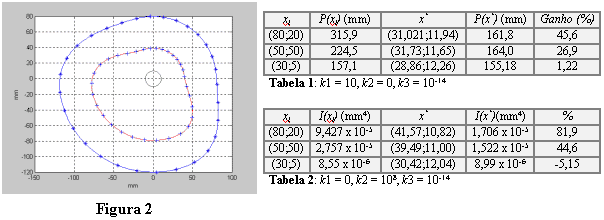
Note que as Tabelas 1 e 2 apresentam, respectivamente, resultados para a minimização do perímetro e para a minimização do momento de inércia.
Em todos os resultados obtidos, as restrições de desigualdade (19) foram respeitadas. Ou seja, tratam-se de restrições inativas. Isto significa que, pelo menos para algumas condições de projeto, a desconsideração das mesmas na implementação do algoritmo, com a sua verificação a posteriori, é uma estratégia válida. Os ganhos percentuais obtidos, tanto a minimização do perímetro, como para a minimização do momento de inércia, comprovam a efetividade do procedimento.
REFERENCIAS BIBLIOGRÁFICAS:
[1] Chen, F.Y.- Mechanics and Design of Cam Mechanisms, Pergamon Press, New York, 1982.
[2] Mabie, H.H.; C. F. Reinholtz -Mechanisms and Dynamics of Machinery, Jonh Wiley & Sons, New York, 1985.
[3] Johnson, K. L. Contact Mechanics, Cambridge University Press, Cambridge, 1985.
[4] Luenberger, D. G., Linear and Nonlinear Programing, Addison-Wesley Publishing Company, Stanford, 1989.