USO DE ALGORITMOS GENÉTICOS PARA APLICAÇÕES EM PROBLEMAS DE OTIMIZAÇÃO DE SISTEMAS MECÂNICOS
PETRIELLI, M. L.
LIMA Jr., J. J.
Departamento de Mecânica, Escola Federal de Engenharia de Itajubá, EFEI, Av. BPS 1303, 37500-903, Itajubá, MG, mauricio.petri@bol.com.br
Palavras-chave: Algoritmos Genéticos, Otimização
RESUMO
Neste trabalho é apresentado um estudo, de caráter exploratório, sobre Algoritmos Genéticos (Genetic Algorithms - GAs). Os GAs são métodos de otimização que nos últimos vem ganhando importância como ferramenta na busca de soluções, em problemas de otimização complexos, devido a sua facilidade de implementação e habilidade de encontrar a solução onde alguns métodos apresentam deficiência. Para enfatizar a eficácia dos GAs são apresentados exemplos, utilizando os programas desenvolvidos neste trabalho, tanto na otimização de algumas funções matemáticas quanto na solução de problemas clássicos de sistemas mecânicos.
O que são os GA's?
Algoritmos Genéticos (GA's) são métodos computacionais de busca baseados nos mecanismos de evolução natural e na genética. Em GA's uma população de possíveis soluções para o problema em questão evolui de acordo com operadores probabilísticos concebidos a partir de metáforas biológicas, de modo que há uma tendência de que, na média, os indivíduos representam soluções cada vez melhores à medida que o processo evolutivo continua.
Como funciona os GA's?
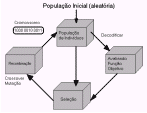
Um algoritmo genético emprega três operadores básicos: (1) Seleção; (2) Recombinação; (3) Mutação.
Processo de Seleção
Utilizando o método da roleta, que prioriza os indivíduos que contenha os maiores valores de adequabilidade, pode-se selecionar os melhores indivíduos para a composição da melhor população global.
Processo de Recombinação
A partir dos indivíduos selecionados na roleta fixa-se uma posição aleatória para o cruzamento dos genes envolvidos nesse cromossomo. Combinando esses cromossomos obtém-se uma nova população, que pode, ou não, ser a melhor
Antes: X1 = [ 0 0 0 0 1 0 0 1 ] X2 = [ 0 1 0 1 0 1 1 0 ]
Depois: X1'= [ 0 0 0 0 0 1 1 0 ] X2'= [ 0 1 0 1 1 0 0 1 ]
Processo de Mutação
Seleciona-se uma posição aleatória num cromossomo e muda-se o valor do gene correspondente por um outro gene possível.
Antes: X1'= [ 0 0 0 0 0 1 1 0 ]
Depois: X1"= [ 0 0 1 0 0 1 1 0 ]
Como resultado dessa pesquisa é apresentado um programa computacional de otimização usando a técnica dos GAs. Através da otimização de algumas funções matemáticas e da otimização de sistemas mecânicos, utilizando o programa desenvolvido, pode-se comprovar a alta eficiência dos GAs.
Exemplos de Aplicação

Aplicação na Mecânica: Posicionamento Ótimo de Sensores e Atuadores
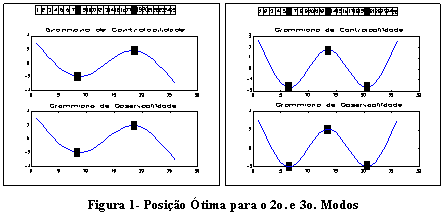
Para mostrar a eficiência do método, foi usado uma estrutura do tipo viga com condição de contorno livre nas extremidades, constituído de 25 elementos finitos do tipo viga de Euller-Bernoulli. Nosso propósito é determinar o posicionamento ótimo para a colocação do atuador e sensor, de modo que se obtenha o mínimo esforço do controlador ou a máxima energia de saída. Isto é conseguido através da busca de mínimos e máximos utilizando a rotina de Algoritmo Genético desenvolvida.
A Figura 1 mostra o posicionamento ótimo para a colocação de um atuador na viga de maneira a controlar o segundo e terceiro modos de vibração da mesma. Observa-se, que a localização ótima coincide com o ponto de deflexão máxima na estrutura.
Com os estudos realizados e com os resultados apresentados pelo programa desenvolvido, verificou-se a eficiência da técnica de otimização utilizando o conceito de Algoritmos Genéticos. Com base nos trabalhos consultados pode-se afirmar que os GAs vieram para ficar; não sendo portanto uma "técnica da moda", tal afirmação é suportada pela imensa quantidade de aplicações bem sucedidas.
Agradecimentos: os autores agradecem à CNPq, através do Programa Institucional de Iniciação Científica, PIBIC, pelo apoio financeiro, que possibilitou o desenvolvimento dessa pesquisa.
REFERÊNCIAS BIBLIOGRÁFICAS:
GOLDBERG, D. E. (1997), Genetic Algorithms in Search, Optimization, and Machine Learning, Addison Wesley Longman, 412p.